Entradas

Ley de deno y coseno

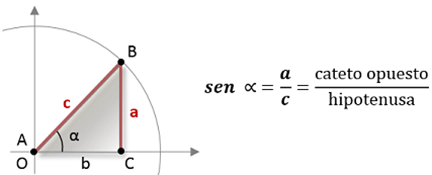
Imagen
Seno El Seno de un ángulo α (sen α) es la razón entre el cateto opuesto al ángulo y la hipotenusa: Ejercicio de Seno: Sea una carretera de montaña con un ángulo de subida de 5º. Calcular cuantos metros de altura sube un vehículo al avanzar un kilómetro (mil metros) por la carretera. Solución: Representamos la carretera y su pendiente como un triángulo con un ángulo de 5º: Por trigonometría sabemos que el seno relaciona el cateto opuestro con la hipotenusa, en este caso la altura con la longitud de la carretera (1000m). Despejamos la altura ya que es la variable que no conocemos: sen 5 = cateto opuesto / hipotenusa = altura / 1000 metros altura = sen 5 · 1000m sen 5 =  0,08751 (lo obtenemos con una calculadora científica) altura = 0,08751 · 1000 = 87, 15 metros Es decir, cada kilómetro (1000 m) que avanza el vehículo cuesta arriba, asciende una altura vertical de 87,15 metros. Coseno La ley de los cosenos es la relación entre las longitudes de los lados de un triáng
Publicar un comentario
Leer más

SESION 6. ECUACIONES

Imagen
  ECUACIONES   ¿Qué es una ecuación? Una ecuación en matemática se define como una igualdad establecida entre dos expresiones, en la cual puede haber una o más incógnitas que deben ser resueltas. Las ecuaciones sirven para resolver diferentes problemas matemáticos, geométricos, químicos, físicos o de cualquier otra índole, que tienen aplicaciones tanto en la vida cotidiana como en la investigación y desarrollo de proyectos científicos. ¿Cuáles son las partes de una ecuación?   Las partes de una ecuación son   Miembros de la ecuación : son cada una de las dos expresiones algebraicas que están separadas por el signo igual (=). ·        Términos de una ecuación : son cada uno de los elementos que forman los miembros de la ecuación. ·        Incógnita de la ecuación : corresponde a la variable (o letra) que aparece en la ecuación. ·        Grado de la ecuación : se trata del mayor exponente que tiene la incógnita de la ecuación. ·        Solución de la ecuación : consi
Publicar un comentario
Leer más

SESION 5. AREA DE UN CIRCULO

Imagen
Área de un circulo El área de un círculo es la medida de la superficie que ocupa, en otras palabras es la cantidad de unidades cuadradas que caben en su interior. La fórmula con la que obtiene el área es: A =  π r 2 Donde  A  se refiere al área,  r  al radio y  π  es el número 3.1415926... Lo que esta fórmula dice es que debes multiplicar al radio por él mismo, y luego multiplicar por una aproximación al valor de π (aquí usaremos π = 3.14). Para sacar el área de un círculo debemos conocer cuánto mide su radio o su diámetro. Recuerda que el radio es la distancia del centro a cualquier punto de la circunferencia, mientras que el diámetro es lo que mide una recta que pasa por el centro y corta a la circunferencia en dos puntos. Con el radio Supongamos que un círculo tiene radio 4 cm. Para sacar su área multiplicamos 4cm por 4cm y luego por 3.14, es decir, el área de un círculo de radio 4 es 50.24 cm 2  (observa la figura siguiente). Aquí puedes observar que cuando el radio
Publicar un comentario
Leer más

SESION4. TEOREMA DE PITAGORAS.

Imagen
Teorema de pitagoras  Surgio en la antigua Babilonia y Egipto en 1900 a.c., quien mismo Piatgoras (matematico y filosofo griego) descubrió que para un triángulo rectángulo, el  cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros lados a 2 +b 2 =c 2 Asi mismo se expersa lo siguente: " En un triángulo rectángulo, la suma del cuadrado de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa"   En este teorema siempres se untilizan los triangulos rectangulos, es decir los que tienen un angulo de 90º, esta figura cuenta con una hipotenusa y catetos, los cuales se clasifican en catetos opuestos y catetos adyacentes.  Por lo que no es nada dificil de respolver a continuacion te mostramos como resolver ejercicios con teoreamas de pitagoras. Para ello resolvemos con ayuda de la siguiente fórmula  c 2= a 2 +b 2 1.       Como se observo en la figura nos pide hallar la hipotenusa por lo que usamos la forula para ubicar los datos. 2.
Publicar un comentario
Leer más

Sesion 3. Angulos

Imagen
Angulos  El ángulo es  la porción del plano comprendida entre dos semirrectas (lados) con un origen común llamado vértice . Los ángulos parten de un punto y tienen dos líneas que salen desde ese punto y que generan una apertura representada por un arco. El grado de apertura de esos arcos (y no su extensión) está representado por el ángulo . Se pueden clasificar de diferentes maneras, ya sea por la medida de su amplitud y según su relación con otros ángulos, por su posición que ocupen por el vértice o la suma de entre ellos.   Clasificación según su amplitud o medida Ángulo nulo :  Es aquel que tiene un valor único, mide 0°. Algunos refieren que tiene un significado conceptual por no existir, debido a que no llega a formar un ángulo. Ángulo agudo : son aquellos ángulos cuya amplitud es mayor a 0° y menor a 90°. Las semirrectas que lo conforman no llegan a ser perpendiculares. Tanto  angulo "a" , como  angulo "b" , son menores a 90° pero mayores a 0°, siendo a
Publicar un comentario
Leer más